| Definitions |  x:A. B(x), x:A. B(x),  , x(s), P , x(s), P   Q, P & Q, t Q, P & Q, t  T, T,  , ,  A, (r/s), P A, (r/s), P    Q, P Q, P   Q, Q,  T, True, T, True,  x:A. B(x), A c x:A. B(x), A c B, S B, S  T, suptype(S; T), {i..j T, suptype(S; T), {i..j }, Outcome, Top, i }, Outcome, Top, i  j < k, A j < k, A  B, B,   x. t(x), t.1, t.2, False, p-open(p), measure(C) x. t(x), t.1, t.2, False, p-open(p), measure(C)  q, i q, i 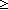 j , RandomVariable(p;n), X j , RandomVariable(p;n), X  Y, rv-const(a), A Y, rv-const(a), A  B, r B, r  s, if b then t else f fi , q_le(r;s), SQType(T), {T}, tt, a s, if b then t else f fi , q_le(r;s), SQType(T), {T}, tt, a  b, b,  b, x f y, b, x f y,   , < , <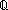 +>, p +>, p   q, qpositive(r), r - s, r + s, r * s, i <z j, ff, qeq(r;s), (i = q, qpositive(r), r - s, r + s, r * s, i <z j, ff, qeq(r;s), (i =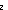 j), s j), s  C, nullset(p;S), FinProbSpace, Dec(P), P C, nullset(p;S), FinProbSpace, Dec(P), P  Q, Q,  , Unit, SqStable(P), (X(n) , Unit, SqStable(P), (X(n)  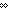 as n as n  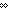 ), ),  |
| Lemmas | nat wf, rv-le wf, rv-const wf, int inc rationals, qless wf, expectation wf, int seg wf, le wf, rationals wf, random-variable wf, finite-prob-space wf, qless transitivity 2 qorder, qle weakening eq qorder, qless irreflexivity, qinv-positive, not functionality wrt iff, assert wf, qeq wf2, assert-qeq, int-rational, qmul preserves qless, qdiv wf, qmul wf, squash wf, true wf, qmul comm qrng, qinv wf, qmul zero qrng, qmul assoc qrng, qmul one qrng, Markov-inequality, rv-qle wf, not wf, bool wf, qmul com, qdiv-qdiv, qmul-qdiv-cancel2, qless transitivity 1 qorder, p-open wf, p-measure-le wf, p-outcome wf, qle wf, p-open-member wf, top wf, subtype rel self, length wf1, decidable ex int seg, subtype rel function, length wf nat, false wf, decidable cand, decidable lt, decidable qle, decidable wf, iff wf, decidable int equal, nat properties, ge wf, expectation-monotone-in-first, expectation-monotone, q le wf, bnot wf, iff transitivity, eqtt to assert, assert-q le-eq, eqff to assert, assert of bnot, qle transitivity qorder, sq stable from decidable, decidable qless, rv-unbounded wf |